Die Grundregel kann immer angewendet werden. Sie liefert unabhängig von der Kardinalität der Beziehung stets drei Tabellen für eine binäre Beziehung. Es gibt Sonderfälle, in denen eine ER-Beziehung zwischen zwei Entity-Typen auf lediglich zwei Relationen oder gar nur eine Relation abgebildet werden können. Diese Sonderfälle können bei 1:n- und 1:1-Beziehungen auftreten, nicht aber bei n:m-Beziehungen.
Das bisher benutzte Maß für eine Kardinalität (nach Chen) ist allerdings zu grob, um eine Entscheidung darüber treffen zu können, ob man mit weniger Tabellen auskommt.
In dem oben dargestellten Beispiel (Grundregel) funktioniert die Zusammenfassung, weil jeder Schüler genau einen Tutor hat. In der Beziehung IstTutor kommt jede Schülernummer genau einmal vor. Bei den Lehrernummern ist das anders. Lehrernummern können in der Tabelle keinmal, einmal oder mehrmals vorkommen. Keinmal kommt sie für Lehrer ohne Tutorengruppe vor, mehrmals für Lehrer mit Tutorengruppe.
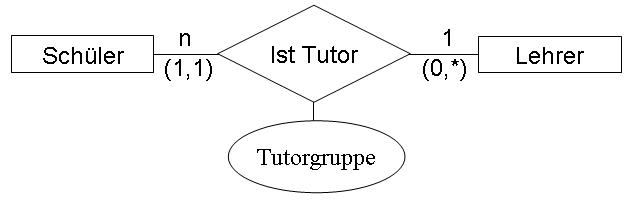
Ausgehend von dieser Beobachtung wird die Kardinalität einer Beziehung in der Theorie auch durch Angabe von minimaler und maximaler Anzahl, mit der jeweils ein Entity-Typ in einer Beziehung vorkommt, angegeben. Ein Schüler kommt in der Beziehung IstTutor minimal und maximal einmal vor – Schreibweise (1,1). Ein Lehrer muss in der Beziehung nicht, kann aber mehr als einmal vorkommen – Schreibweise (0,*). Man sagt auch, dass Schüler obligatorisch (zwingend) in der Relation vorkommen, Lehrer hingegen optional.
Über die obligatorische bzw. optionale Mitgliedschaft an einer Relation müssen in den Geschäftsregeln während des konzeptionellen Entwurfs Aussagen gemacht werden. Innerhalb eines ER-Diagramms können diese Aussagen mithilfe der min-max-Notation gekennzeichnet werden.
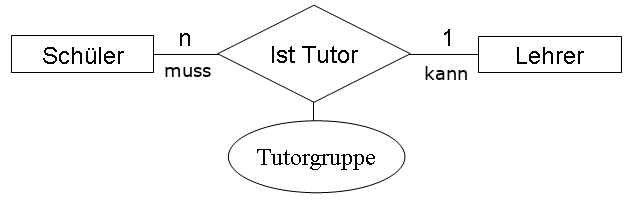
In den Vorgaben des KCGO Informatik wird für die untere Grenze eine andere Notation vorgegeben: eine obligatorische Teilnahme an einer Relation wird mit muss gekennzeichnet, eine optionale mit kann.
Zusammenfassung
Als Mindestzahl interessieren im Wesentlichen 0 und 1 (obwohl es sicher auch Modelle gibt, bei denen die Mindestzahl 2 oder eine noch größere Zahl eine Rolle spielen).
0 – optional
d. h. es kann Elemente aus dem Entity-Typ 1 geben, für die kein Element aus dem Entity-Typ 2 in der Relation R (Assoziation) steht.
Beispiel: Ein Mann kann verheiratet sein mit einer Frau.
1 – obligatorisch
d. h. für jedes Element aus dem Entity-Typ 1 muss es ein Element aus dem Entity-Typ 2 in der Relation R (Assoziation) geben.
Beispiel: Ein Auto muss ein Kfz-Kennzeichen haben.
Als Höchstzahl unterscheiden wir nur zwischen „höchstens 1“ und „keine Einschränkung“ (obwohl es sicher auch Modelle gibt, bei denen andere Einschränkungen eine Rolle spielen).
1 – eindeutig
d. h. für jedes Element aus dem Entity-Typ 1 kann höchstens ein Element aus dem Entity-Typ 2 in der Relation R (Assoziation) existieren.
Beispiel: Ein Auto hat höchstens ein Kfz-Kennzeichen.
* – mehrdeutig
d. h. es kann Elemente aus dem Entity-Typ 1 geben, für die mehr als ein Element aus dem Entity-Typ 2 in der Relation R (Assoziation) existieren.
Beispiel: Eine Bestellung enthält mindestens einen Artikel. Ein Artikel kann Teil einer Bestellung sein.
Hinweis: In der Literatur gibt es keine einheitliche Regelung, auf welcher Seite die Kardinalitäten und Optionalitäten eingetragen werden. Wir haben diese bisher jeweils zum entsprechenden Entity-Typ geschrieben (z.B. wären in der Relation IstTutor die Aussagen 1 Lehrer ist Tutor für n Schüler und Für n Schüler gibt es 1 Lehrer als Tutor möglich). Für die Angabe der Kardinalitäten mit Minimum- und Maximumwerten bietet sich ebenfalls das Eintragen direkt am entsprechenden Entity-Typ an. Analog gilt dies auch für kann- bzw. muss-Angaben.