Aufgabe 1 (Fahrkartenautomat)
Ein Fahrkartenautomat gibt Fahrkarten für die Tarifzonen I und II aus. Es können 50 Cent und 1 € Münzen eingeworfen werden. Die Fahrkarte der Tarifzone I kostet 1,50 €, die der Tarifzone II 2,00 €. Die Fahrkarte wird vor Eingabe des Geldes gewählt und sofort ausgegeben, wenn der passende Betrag eingeworfen wurde. Wird der Fahrpreis überzahlt, dann fällt die entsprechende Münze in das Geldrückgabefach einfach zurücke. Mit einer Korrekturtaste können die Eingaben korrigiert werden.
- Geben Sie alle möglichen Zustände, Eingaben und Ausgaben an.
- Entwerfen Sie den Übergangsgraphen des Automaten.
- Modellieren und testen Sie diesen Graphen in FLACI.
- Implementieren Sie den Automaten in Java.
Aufgabe 2 (Pawlov)
In seinem klassischen Lehrbuch analysierte Pawlov bei Hunden den Zusammenhang zwischen Reiz und Reaktion. Beim Anblick oder Geruch von Futter sonderte der Hund in verstärktem Maße Speichel ab. Wenn wiederholt und in kurzen Pausen – zusammen mit dem Futter – ein neutraler Reiz (Glockenton) geboten wurde, so floss der Speichel nach einiger Zeit auch allein auf den Glockenton hin. Dieser Konditionierungsvorgang lässt sich im Modell des endlichen Automaten erfassen.
Hinweis: Die Menge der Eingabezeichen des Automaten sei {W, G, WG} mit W für Wurst, G für Glocke und WG für die gleichzeitige Darbietung von Wurst und Glocke. Ausgabemenge ist {S} mit S für Speichelfluss. Die Zustände bilden die Menge {z0, z1, z2, z3}, wobei z0 bedeutet, dass der Hund nicht konditioniert ist und z1 bis z3 verschiedene Stufen der Konditionierung symbolisieren.
- Geben Sie einen Übergangsgraphen an.
- Modellieren Sie den Automaten in FLACI.
- Implementieren Sie den Graphen in Java.
Aufgabe 3 (Einarmiger Bandit)
Als einarmigen Banditen bezeichnet man einen Glücksspielautomat, bei dem nach Einwurf einer Münze und Betätigen eines Hebels drei nebeneinander liegende Walzen kurzzeitig in Rotation versetzt werden. Auf jede Walze sind verschiedene Symbole aufgedruckt. Beim Stillstand der Walzen erscheint jeweils eines der Symbole in einem Sichtfenster. Gewonnen wird, wenn bestimmte Symbolkombinationen in den Sichtfenstern der einzelnen Walzen erscheinen.
Betrachte einen vereinfachten „einarmigen Banditen“, der lediglich zwei Walzen besitzt. Auf jede Walze sind die Symbole Apfel, Birne und Krone aufgedruckt. Hat man den Hebel betätigt und es erscheinen zwei Kronen, dann wird der doppelte Einsatz ausgezahlt. Erscheinen zwei gleiche Äpfel oder zwei Birnen, wird der Einsatz zurückgezahlt. Fasse den einarmigen Banditen als Endlichen Automaten auf. Neben „Münzeinwurf 1€“ und „Hebel betätigen“ sollen die im Fenster erscheinenden Symbolkombinationen Eingaben des Automaten sein.
- Geben Sie alle möglichen Zustände, Eingaben und Ausgaben an.
- Entwerfen Sie den Übergangsgraphen des Automaten.
- Was ändert sich, wenn der Automat drei Walzen besitzt?
Aufgabe 4 (Addierer)
Entwickeln Sie einen Mealy-Automaten mit dem Eingabealphabet {X = {0, 1, 2}} und dem Ausgabealphabet {Y = {0, 1, 2, 3, 4, n}}, der zwei Ziffern addiert und die Summe ausgibt. Beispiele: 01→1, 22→4. Danach soll sich der Automat wieder im Startzustand befinden.
Geben Sie einen geeigneten Übergangsgraphen an und testen Sie diesen in FLACI.
Aufgabe 5 (Serienaddierer)

Gesucht ist ein Automat, der zwei Dualzahlen stellenweise, beginnend mit dem niederwertigsten Bits, addiert – ein Serienaddierer. Dabei werden die jeweils an dem Eingang des Automaten liegenden Dualziffern zum nächsten Bit des Ergebnisses zusammengefasst.
- Führen Sie die dargestellte Addition per Hand durch.
- Entwerfen Sie einen Automaten für einen solchen Addierer.
- Implementieren Sie diesen Automaten in einem Java-Programm und in FLACI.
- Der Käfer Kara soll zwei Dualzahlen addieren …
Aufgabe 6 (Dualtaschenrechner)
Beschreiben Sie einen einstelligen Dualtaschenrechner als endlichen Automaten. Der Rechner soll über die Grundrechenarten Addition und Multiplikation verfügen, ist aber in seinem Zahlbereich extrem eingeschränkt: eingegeben werden nur die Dualzahlen 0 und 1, als Ergebnis zur weiteren Arbeit wird nur die Einerziffer des dualen Ergebnisses ausgegeben; z. B. ergibt die Rechnung 1+1 eine 0, da die führende Eins des Ergebnisses (10) weggelassen wird.
Aufgabe 7 (modulo)
Gesucht ist eine Zählschaltung modulo 3 (also einen Zähler, der bis zwei Zählen kann: 1-2-0-1-2-0-…). Zusätzlich soll der Zähler durch die Eingabe von Reset in den Anfangszustand zurückgesetzt werden können. Der Zähler ändert seinen Zustand, wenn
- Variante: ein Taktsignal T eintrifft
- Variante: die Eingabe von 1 auf 0 wechselt (Takt bei fallender Flanke)
Geben Sie die Übergangsgraphen an und simulieren Sie die beiden Varianten jeweils in FLACI und in Java.
Aufgabe 8 (Prüfbitgenerator)
Entwickeln Sie einen Prüfbitgenerator. Da die meisten Zeichensätze weniger als 128 Zeichen enthalten, können sie als siebenstellige Dualzahl kodiert werden. Das eigentlich überflüssige achte Bit kann als Prüfbit genutzt werden, das bei der Datenübertragung zur Fehlererkennung genutzt wird. Eine Möglichkeit Prüfbits zu erzeugen, ist die, an die zu übertragenden Zeichen jeweils eine 1 oder 0 so anzuhängen, dass das gesendete Byte immer eine gerade Anzahl von Einsen enthält (gerade Parität). Der gesuchte Automat soll nun nacheinander 7 Bits einlesen, diese wieder ausgeben und dann das entsprechende Prüfbit anhängen.
- Modellieren Sie einen geeigneten Automaten und testen Sie diesen in FLACI und in einem Java-Programm.
- Bei dieser Aufgabe könnte man darüber nachdenken, wie Kara das Problem wohl lösen würde …
Aufgabe 9 (Caesar)
Entwickeln Sie einen Mealy-Automaten mit dem Eingabealphabet
{X = {a, b, c, d}}, der bei der Ausgabe die eingegebenen Zeichen zyklisch vertauscht (Cäsar-Verschlüsselung).
Beispiel: badcadcc → cbadbadd
Geben Sie einen Übergangsgraphen an und testen Sie diesen in FLACI.
Aufgabe 10 (Spielzeug)
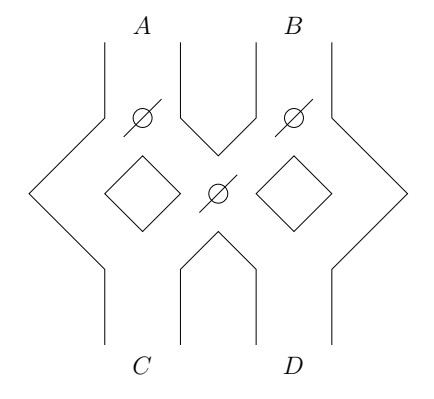
Betrachten wir das nebenstehende Spielzeug.
Eine Kugel wird in A oder B eingeworfen. Je nach Ausrichtung der drei Weichen fällt
die Kugel nach links oder rechts. Immer wenn, eine Kugel auf eine Weiche trifft, bewirkt
dies eine Richtungsänderung der Weiche – die nächste Kugel, die auf die Weiche trifft, fällt also auf die andere Seite.
Es ist ein Transduktor zu modellieren, der über dem Eingabealphabet X = \{a, b\} und dem Ausgabealphabet Y = \{c, d\} ein (dauerhaftes) Spielen simuliert. Startzustand soll der abgebildete Zustand sein.
Hinweis: Überlege wie viele Zustände für die Weichen insgesamt möglich sind.

