Aufgabe 1 (lineare Gleichung)
Gegeben ist eine lineare Gleichung der Form y = ax + b. Nach Eingabe der Parameter a und b und des Funktionswertes y soll der Wert für die Variable x berechnet werden.
- Erstellen Sie einen Algorithmus (Pseudocode und Struktogramm).
- Implementieren Sie ein geeignetes Programm in Java.
Aufgabe 2 (quadratische Gleichung)
Gegeben ist eine quadratische Gleichung in der Form y = ax² + bx + c. Gesucht ist ein Java-Programm, welches nach Eingabe der Parameter a, b und c die Lösungen bzw. geeignete Bemerkungen ausgibt.
Aufgabe 3 (Fehlersuche)
Gegeben ist das folgende (fehlerhafte Java-Programm):
public class Beispiel01 {
public static void main(String[] args) {
int kundennummer, anzahl;
double preis, gesamtpreis;
System.out.print("Geben Sie Ihre Kundennummer ein: ");
Input.readInt(kundennummer);
System.out.print("Geben Sie die Anzahl ein: ");
System.out.print("Geben Sie den Stückpreis ein: ");
Input.readDouble(preis);
preis * anzahl = gesamtPreis;
if (kundennummer < 100) {
gesamtPreis = gesamtPreis * 0.95
}
if (anzahl < 20) {
gesamtPreis = gesamtPreis + 15;
} else
if (anzahl < 50) {
gesamtPreis = gesamtPreis + 5;
}
}
}
- Im Quelltext befinden sich 6 Fehler (syntaktisch als auch logisch). Finden Sie diese und ergänzen Sie bei Bedarf. Implementieren Sie das Java-Programm.
- Geben Sie für den vorliegenden Text (incl. der Änderungen aus a)) ein Struktogramm an.
- Finden Sie für das Programm eine geeignete Aufgabenstellung
Aufgabe 4 (Werkzeugladen)
In einem Werkzeugladen werden folgende Preise verlangt
- 5 Cent pro Schraube
- 3 Cent pro Mutter
- 1 Cent pro Unterlegscheibe
Implementieren Sie ein Java-Programm, das den Anwender nach der Anzahl der Schrauben, Muttern und Unterlegscheiben fragt und dann den Gesamtbetrag berechnet und ausgibt.
Zusätzlich überprüft das Programm die Bestellung. Es ist normalerweise ein Fehler, wenn mehr Schrauben als Muttern bestellt werden. In diesem Fall gibt das Programm die Meldung aus „Kontrollieren Sie Ihre Bestellung!“. Andernfalls gibt das Programm aus „Die Bestellung ist okay.“ In jedem Fall wird der Gesamtbetrag ausgegeben.
Aufgabe 5 (Versandgeschäft)
Ein Versandgeschäft berechnet bei Aufträgen bis zu 100 € einen Verpackungszuschlag von 3 € und einen Portoanteil von 2 €. Bei Rechnungsbeträgen von 100 € bis zu 200 € liefert es zwar portofrei, berechnet jedoch einen Verpackungszuschlag von 2 €. Kauft der Kunde für 200 € und mehr, so entstehen ihm keine zusätzlichen Kosten.
- Geben Sie einen Algorithmus für die Berechnung der Kosten im Pseudocode und als Struktogramm an.
- Implementieren Sie ein entsprechendes Java-Programm.
Aufgabe 6 (Schaltjahr)
Ein Schaltjahr findet alle 4 Jahre statt … leider falsch. Für die genaue Regelung gibt es einige Verfeinerungen. Das abgebildete Struktogramm stellt die genaue Schaltjahrregelung dar.
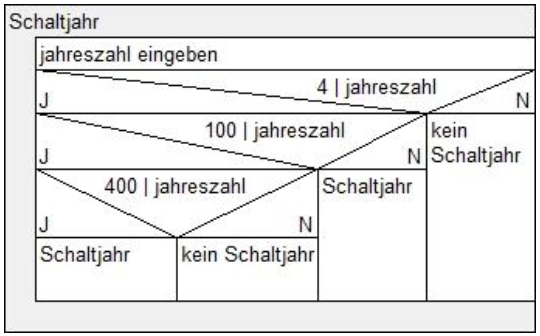
Implementieren Sie mithilfe des gegebenen Struktogramms ein Java-Programm, welches für ein eingegebenes Jahr angibt, ob es ein Schaltjahr ist.
Hinweis: 4 \mid \text{jahreszahl} bedeutet „4 teilt die jahreszahl“, d. h. man müsste testen, ob die Jahreszahl durch 4 ohne Rest teilbar ist. (Kleine Tipps und Tricks)
Aufgabe 7 (Gewicht)
Ein Programm soll helfen, zu entscheiden, ob eine Person über-, unter- oder normalgewichtig ist. Als Eingabedaten werden Geschlecht, Alter, Gewicht und Größe verlangt.
Als normalgewichtig bezeichnet man Personen, deren Gewicht in Kilogramm gleich der Körpergröße über 100 cm ist. Entsprechend ergeben sich die Unter- bzw. Übergewichtigen.
Als Toleranzgrenzen sind bei Frauen +4% bis -7% und bei Männern +5% bis -5% Abweichung von den Sollwerten zugelassen.
Alle Aussagen treffen erst für Personen zu, deren Wachstum beendet ist, d. h. die älter als 17 Jahre und größer als 1,20 m sind. Bei anderen Personen können keine Angaben gemacht werden.
Implementieren Sie ein Java-Programm für das gegebene Problem.
Aufgabe 8 (Maximum)
In einem Konsolenprogramm sollen drei Zahlen eingegeben werden. Das Programm soll die größte der drei Zahlen ausgeben.
Erweitern Sie die Ausgabe in der Form, dass die Zahlen der Größe nach geordnet ausgegeben werden.
Implementieren Sie als Erweiterung auch ein GUI-Programm zu dieser Problemstellung.
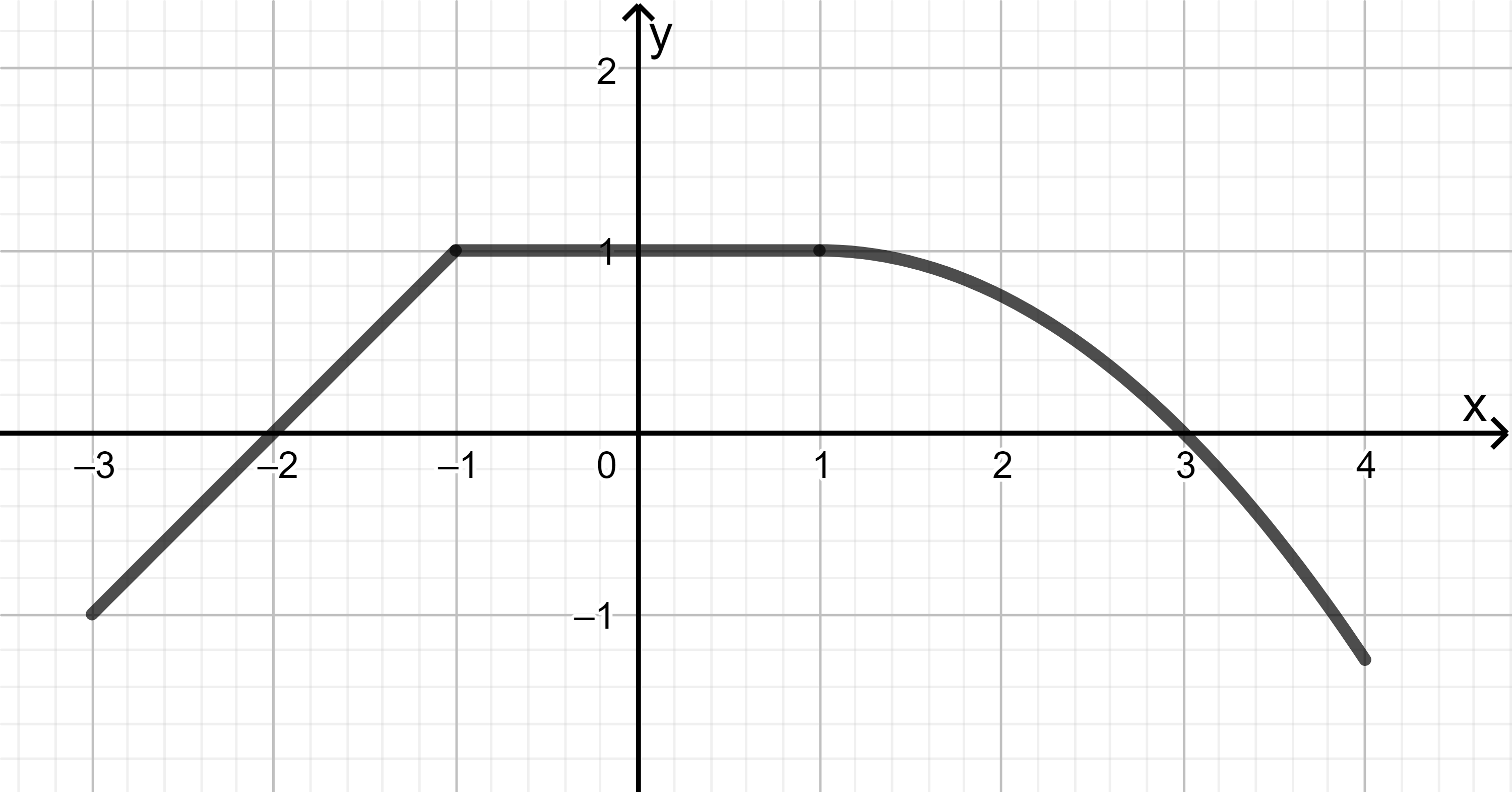
Aufgabe 9 (abschnittsweise definierte Funktion)
Implementiere ein Java-Programm, welches für einen eingegebenen Wert x den entsprechenden Funktionswert ausgibt.
Aufgabe 10 (Schnittpunkt)
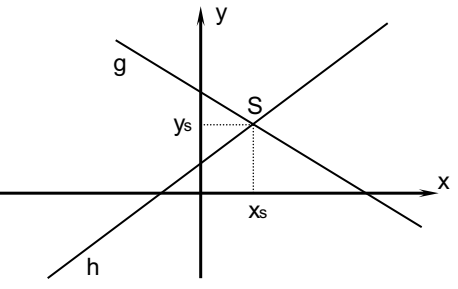
Zwei Geraden g und h werden durch die Gleichungen {g(x) = y= ax + b} und {h(x) = y= cx + d} beschrieben.
Implementieren Sie ein Java-Programm, welches mit Hilfe der eingegebenen Koeffizienten a, b, c und d den Schnittpunkt der beiden Geraden berechnen kann. Dabei sollen möglichst alle Lagebeziehungen zweier Geraden zueinander berücksichtigt
werden. Erstellen Sie vorher ein Struktogramm.
Aufgabe 11 (Scheinausgabe)
Implementieren Sie ein Programm, welches zu einem vorgegebenen Geldwert ausrechnet, mit welchen Geldscheinen man ihn auszahlen kann. Zur Auszahlung stehen Scheine im Wert von 500, 200, 100, 50, 20, 10
und 5 Euro zur Verfügung.
Hinweis: Für integer-Variablen gibt es zwei mathematische Operationen für die Division, da wir ja auf Kommazahlen verzichten müssen:
- Bestimmung des ganzzahligen Anteils: 11 / 5 hat das Ergebnis 2, da die 5 2x in die Zahl 10 passt.
- Bestimmung des Restes bei der Division (Modulo): 11 % 5 hat das Ergebnis 1, da bei der Division der Rest 1 entsteht.
Die Programmausgabe könnte so aussehen:
Wie groß ist der Geldbetrag: 2215
500er-Scheine: 4
200er-Scheine: 1
100er-Scheine: 0
50er-Scheine: 0
20er-Scheine: 0
10er-Scheine:1
5er-Scheine: 1

