Umsetzung einer 1:n-Beziehung
Betrachten wir die Umsetzung einer 1:n-Beziehung an einem Beispiel (Attribute nur teilweise dargestellt):

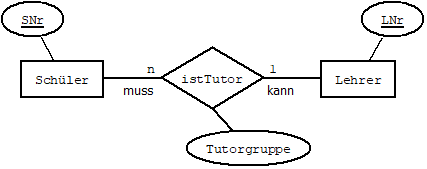
Ein Schüler kommt in der Beziehung IstTutor minimal und maximal einmal vor (genau einmal). Ein Lehrer muss in der Beziehung nicht, kann aber mehr als einmal vorkommen. Die Grundregel liefert folgendes Relationenschema:
Schüler ( SNr, Name, Vorname, …)
Lehrer ( LNr, Name, Vorname, …)
istTutor ( ↑SNr, ↑LNr, Tutorgruppe)
Diese Tabellen dürfen zu zwei Tabellen verbunden werden. Da jeder Schüler genau einen Lehrer als Tutor hat, werden die Spalten der istTutor-Tabelle in die Tabelle Schüler übernommen. Das Attribut LNr in der Relation Schüler ist ein Fremdschlüssel.
Schüler ( SNr, Name, Vorname, …, ↑LNr, Tutorgruppe)
Lehrer ( LNr, Name, Vorname, …)
Ist bei einer ER-Beziehung der Kardinalität 1:n zwischen den Entity-Typen E1 und E2 der Entity-Typ E2 (n) obligatorisch in der Beziehungsrelation B, so können die Relationenschemata von E2 und B zu einem Schema verbunden werden. Zur Abbildung benötigt man nur zwei Tabellen.
Betrachten wir nun ein Beispiel für eine optionale Beziehung:


Ein Ausleiher kann minimal 0, maximal mehr als ein Buch ausleihen; ein Buch kann nicht oder maximal einmal ausgeliehen werden. Die Grundregel liefert folgendes Relationenschema:
Buch ( BNr, Titel, Autor, …)
Ausleiher ( ANr, Name, …)
leihtAus ( ↑BNr, ↑ANr, Leihdatum)
Auch diese Tabellen kann man zu zwei Tabellen zusammenfassen. Dabei wird die leihtAus-Tabelle in die Tabelle Buch übernommen. Allerdings können in dieser entstandenen Relation bei nicht ausgeliehenen Büchern Nullwerte entstehen (und zwar bei jedem Buch, welches nicht ausgeliehen ist).
Buch ( BNr, Titel, Autor, …, ↑ANr, Leihdatum )
Ausleiher ( ANr, Name, …)
Da die hier entstandenen Nullwerte durchaus sinnvoll interpretiert werden können („Ein Buch ist momentan nicht ausgeliehen.“), ist diese Zusammenfassung durchaus möglich.
Allerdings sollte man trotzdem versuchen bei einem Datenbankentwurf Nullwerte zu vermeiden. Sie sind Ursache unnötiger Komplikationen. Eine (zusammengefasste) Tabelle Buch könnte z. B. so aussehen:
| BNr | Titel | Autor | ANr | Leihdatum |
| 3600312 | Duden Informatik | Schall | 101 | 12.01.20 |
| 3600134 | GK und LK Informatik | Rollke | NULL | NULL |
| 3600135 | Informatik | Goldschläger | 205 | 01.03.20 |
| … | … | … | … | … |
Über dieser Relation sind nun folgende Selektionen möglich:
- \sigma_{ANr < 200} (Buch)
- \sigma_{ANr \geq 200} (Buch)
- \sigma_{ANr < 200} (Buch) \cup \sigma_{ANr \geq 200} (Buch)
Was bedeuten die jeweiligen Ergebnisse der Selektionen? Ergibt die Mengenvereinigung die ursprüngliche Tabelle?
Wie sieht die Situation aus, wenn z. B. in einer Kundendatei einer Firma die (optionalen) Angaben des Geburtsortes und der Telefonnummer der Kunden erfasst werden sollen:


Ein Kunde wurde minimal und maximal in einem Ort geboren (muss in genau einem Ort); in einem Ort können mehrere oder keiner der Kunden geboren sein. (Ein Kunde kann eine Telefonnummer angeben, muss aber nicht.) Die Grundregel liefert hier folgendes Relationenschema:
Kunde ( KNr, KName, Telefon, …)
Ort ( PLZ, Name, …)
geborenIn ( ↑KNr, ↑PLZ)
Fassen wir auch diese Tabellen nach der oben beschriebenen Regel zusammen:
Kunde ( KNr, Name, Telefon, …, ↑PLZ)
Ort ( PLZ, Name, …)
Da für einen Kunden weder die Telefonnummer, noch der Geburtsort bekannt sein müssen, können auch hier Nullwerte entstehen. Im Gegensatz zur Relation leihtAus sind diese aber nicht sinnvoll interpretierbar.
Eine Telefonnummer kann z.B. nicht bekannt sein, aber auch schlichtweg nicht existieren. Die so entstehenden Nullwerte sind als notwendiges Übel zu betrachten, in diesem Fall aber unproblematisch, da eine mögliche Vereinfachung nicht von diesem Attribut abhängt.
Der Geburtsort kann unbekannt oder dessen Angabe unerwünscht sein. Die fehlende Interpretierbarkeit solcher Nullwerte wird zum Problem, wenn diese in einem Fremdschlüssel auftauchen. Solche Nullwerte sind zwingend zu vermeiden. Daher sind diese Tabellen nicht zusammenfassbar.
Auf eine genaue Definition und die Verarbeitung der beiden Arten von Nullwerten gehen wir an anderer Stelle ein genauer ein.
Ist bei einer ER-Beziehung der Kardinalität 1:n zwischen den Entity-Typen E1 und E2 der Entity-Typ E2 (n) optional in der Beziehungsrelation B, so sollten die Relationenschemata von E2 und B nicht zusammengefasst werden.
In Ausnahmefällen können diese zu einem Schema verbunden werden, wenn die dann zu erwartenden Nullwerte sinnvoll interpretierbar sind.
Umsetzung einer 1:1-Beziehung
Betrachten wir die Umsetzung einer 1:1-Beziehung am Beispiel von Spinden in der Schule:

Die Grundregel liefert folgendes Relationenschema:
Schüler ( SNr, Name, Vorname, …)
Spind ( SpNr, Standort)
besitzt ( ↑SNr, ↑SpNr)
Haben nun alle Schüler einen Spind, sind also Schüler obligatorisch an der besitzt-Beziehung beteiligt, so kann die besitzt-Tabelle mit der Schüler-Tabelle verbunden werden.
Schüler ( SNr, Name, Vorname, …, ↑SpNr)
Spind ( SpNr, Standort)
Hätte jedoch nur ein Schüler keinen Spind (optionale Beziehung), so würde bei diesem Schüler ein Nullwert als Spindnummer auftreten. Ist dieser Nullwert nicht sinvoll interpretierbar (Der Schüler will keinen Spind oder …), dürfen die beiden Tabellen nicht verbunden werden (siehe oben).
Nehmen wir an, es gibt wenige Spinde und viele Schüler, die Spinde wären also obligatorisch an der Beziehung beteiligt. In diesem Fall könnte man die besitzt-Tabelle mit der Spind-Tabelle verbinden, ohne dass Nullwerte entstehen:
Schüler ( SNr, Name, Vorname, …)
Spind ( SpNr, Standort, ↑SNr)
Bleibt jedoch nur ein Spind ungenutzt (optionale Beziehung), so würde bei diesem Spind ein Nullwert als SNr auftreten. Ist dieser Nullwert nicht sinvoll interpretierbar (Der Schlüssel zum Spind fehlt oder kein Schüler will den Spind haben oder …), dürfen die beiden Tabellen nicht verbunden werden (siehe oben).
Wenn bei einer 1:1-Beziehung beide Entity-Typen obligatorisch an der Beziehung teilnehmen, zum Beispiel wenn eine Schule dafür sorgen würde, dass genau jeder Schüler einen Spind hat und zu jedem Spind genau ein Schüler gehört, so können die drei Tabellen zu einer einzigen Tabelle verbunden werden, als Primärschlüssel kann einer der bisherigen Primärschlüssel gewählt werden:
SchülerSpind ( SNr, Name, Vorname, …, SpNr, Standort)
Ist bei einer ER-Beziehung der Kardinalität 1:1 zwischen den Entity-Typen E1 und E2 einer der beiden Entity-Typen obligatorisch in der Beziehungsrelation, so können die Relationenschemata von Ei und B zu einem Schema verbunden werden. Zur Abbildung benötigt man nur zwei Tabellen. Der obligatorische Entity-Typ erhält den Primärschlüssel des anderen Entity-Typen als Fremdschlüssel.
Sind beide Entity-Typen obligatorisch in der Beziehungsrelation, so benötigt man nur eine Tabelle.
Umsetzung einer n:m-Beziehung
Beziehungen der Kardinalität n:m können immer nur auf drei Relationenschemata abgebildet werden. Die beiden beteiligten Entity-Typen werden auf je ein Relationenschema abgebildet, die Grundregel gibt an, wie die Beziehung abgebildet wird. Es ist nicht möglich, zwei der drei entstehenden Tabellen zu verbinden, ohne dass Nullwerte entstehen würden.
Es lohnt sich jedoch, die Beziehung zwischen den Entity-Typen und Beziehungsschemata genauer zu betrachten. Die ER-Beziehung Lehrer unterrichtet Schüler …

… ergibt die Relationen
Lehrer ( LNr, Name, …)
Schüler ( SNr, Name, …)
unterrichtet ( ↑LNr, ↑SNr)
Zwischen Lehrern und den Paaren der unterrichtet-Tabelle besteht eine 1:n-Beziehung, denn jeder Lehrer unterrichtet viele Schüler. Diese Beziehung ist auf der n-Seite obligatorisch, weil ein Lehrer, der einen Schüler unterrichtet, per Konstruktion in der Lehrer-Tabelle enthalten ist. Analoges gilt für die Beziehung zwischen Paaren der unterrichtet-Tabelle und Schülern. Hier besteht eine obligatorische m:1-Beziehung. Man kann also sagen:
Eine ER-Beziehung der Kardinalität n:m kann auf je eine obligatorische 1:n- und m:1-Beziehung aufgeteilt werden.
Umsetzung einer is-a-Beziehung
Die Umsetzung einer is-a-Beziehung kann je nach konkreter Anwendung unterschiedlich sein; generell wird eine is-a-Beziehung jedoch wie eine 1:n-Beziehung behandelt.
Das gezeigte Beispiel spezialisiert Schüler in Ober- und Mittelstufenschüler. Für alle gilt als Primärschlüssel die SNr (exemplarisch wurden einige Attribute ergänzt).

Im Relationenmodell würden hier 3 Relationen benötigt:
Schüler ( SNr, Name)
Oberstufenschüler ( ↑SNr, Tutor, Prüfung1)
Mittelstufenschüler ( ↑SNr, Klasse)
Alternativ können auch alle Attribute der Superklasse in die Subklassen übernommen werden:
Schüler ( SNr, Name)
Oberstufenschüler ( ↑SNr, Name, Tutor, Prüfung1)
Mittelstufenschüler ( ↑SNr, Name, Klasse)
In jeder Relation gilt der Primärschlüssel des Supertyps Schüler, in den Relationen Oberstufenschüler und Unterstufenschüler ist dieser auch ein Fremdschlüssel. Die Attribute des Supertyps tauchen auch in den Relationen der Subtypen Oberstufenschüler und Mittelstufenschüler auf. Praktisch kann es (in diesem Beispiel) jedoch dazu kommen, dass die Relation Schüler nicht mit Datensätzen gefüllt wird …
Umsetzen schwacher Entitäten
Da schwache Entitäten keinen ausreichenden Primärschlüssel enthalten, benötigen diese zusätzlich zum eigenen Primärschlüssel den Primärschlüssel des übergeordneten Entity. Mit dem Beispiel des zitierten Modells …

… ergeben sich folgenden Relationen:
Raum ( ↑GNr, RNr, Größe)
Gebäude ( GNr, Adresse, Etagen)

