Definition: Akzeptor
Ein deterministischer endlicher Automat ohne Ausgabe (Akzeptor) ist ein 5-Tupel {A := ( X, Z, \delta, z_0, Z_E )}, wobei gilt:
– X ist eine nicht leere, endliche Menge, das Eingabealphabet, wobei gilt: {x \in X}
– Z ist eine nicht leere, endliche Menge, die Zustandsmenge, wobei gilt: {z \in Z}
– \delta ist die Überführungsfunktion, welche jedem Paar (Eingabezeichen, Zustand) einen Folgezustand zuordnet: {\delta : X \times Z \rightarrow z}
– {z_0 \in Z} ist der Anfangszustand
– Z_E \subseteq Z ist eine Teilmenge von Z, die Endzustandsmenge
Bemerkung
- ein {x \in X} heißt Eingabezeichen
- ein {z \in Z} heißt Zustand
- die verwendeten Zeichen für die einzelnen Bestandteile eines Akzeptors können (je nach Literatur) abweichen, häufig findet man z. B. auch: {A := ( Q, \Sigma, \delta, q_0, F )}
Funktionsweise und Erklärung
Die Unterschiede zwischen Akzeptor und Transduktor liegen darin, dass ein Akzeptor keine Ausgaben besitzt, aber dafür ein oder mehrere Endzustände (Zu beachten ist hier jedoch, dass in einigen Definitionen auch Transduktoren Endzustände besitzen). Ein Akzeptor akzeptiert und erkennt ein Eingabewort und signalisiert durch seinen Endzustand das Ergebnis nach außen.
Darüber hinaus sind Endzustände nicht als eine Kombination von Sackgasse und Einbahnstraße zu verstehen. Ist der Automat nach dem kompletten Einlesen des Eingabewortes in einem Endzustand, so akzeptiert er das Wort. Ist er nicht in einem Endzustand beim Ende des Wortes, so verwirft er es. Sollte ein Wort noch nicht zu Ende sein und ein Automat erreicht einen Endzustand, wird dieser als „normaler“ Zustand behandelt.
Anschauliche Darstellung
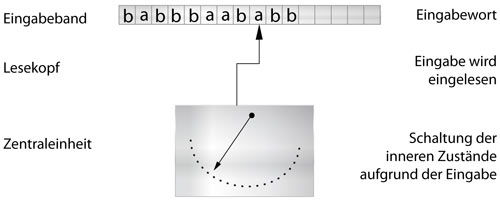
Das Eingabeband wird zeichenweise (von links nach rechts) gelesen. Mit Hilfe des Eingabezeichens und des aktuellen Zustandes wird ein Folgezustand eingestellt.
Darstellung des Automaten
Wie im Abschnitt Darstellung von Automaten beschrieben, gibt es mehrere Möglichkeiten, Automaten darzustellen. Bei der Darstellung von Automaten ist jedoch zu beachten, dass es keine Ausgabefunktion gibt und daher entsprechende Bezeichnungen am Übergangsgraphen und in der Übergangstabelle fehlen.
Beispiel
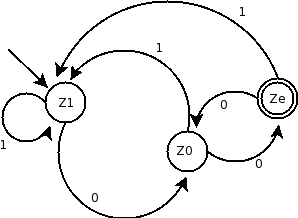
Nebenstehend ist ein einfaches Beispiel für einen Akzeptor über dem Alphabet {X = \{0,1\}}.
Welche Worte werden von diesem Automaten akzeptiert?

